Woodall number
In number theory, a Woodall number (Wn) is any natural number of the form
- Wn = n × 2n − 1
for some natural number n. The first few Woodall numbers are:
- 1, 7, 23, 63, 159, 383, 895, … (sequence A003261 in OEIS).
Woodall numbers were first studied by Allan J. C. Cunningham and H. J. Woodall in 1917, inspired by James Cullen's earlier study of the similarly-defined Cullen numbers. Woodall numbers curiously arise in Goodstein's theorem.
Woodall numbers that are also prime numbers are called Woodall primes; the first few exponents n for which the corresponding Woodall numbers Wn are prime are 2, 3, 6, 30, 75, 81, 115, 123, 249, 362, 384, … (sequence A002234 in OEIS); the Woodall primes themselves begin with 7, 23, 383, 32212254719, … (sequence A050918 in OEIS).
In 1976 Christopher Hooley showed that almost all Cullen numbers are composite. Hooley's proof was reworked by Hiromi Suyama to show that it works for any sequence of numbers n · 2n+a + b where a and b are integers, and in particular also for Woodall numbers. Nonetheless, it is conjectured that there are infinitely many Woodall primes. As of December 2007[update], the largest known Woodall prime is 3752948 × 23752948 − 1.[1] It has 1,129,757 digits and was found by Matthew J. Thompson in 2007 in the distributed computing project PrimeGrid.
Like Cullen numbers, Woodall numbers have many divisibility properties. For example, if p is a prime number, then p divides
- W(p + 1) / 2 if the Jacobi symbol
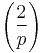 is +1 and
is +1 and
- W(3p − 1) / 2 if the Jacobi symbol
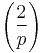 is −1.
is −1.
A generalized Woodall number is defined to be a number of the form n × bn − 1, where n + 2 > b; if a prime can be written in this form, it is then called a generalized Woodall prime.
See also
- Mersenne prime - Prime numbers of the form 2n − 1.
References
- ^ "The Prime Database: 938237*2^3752950-1", Chris Caldwell's The Largest Known Primes Database, http://primes.utm.edu/primes/page.php?id=83407, retrieved December 22, 2009
Further reading
- Guy, Richard K. (2004), Unsolved Problems in Number Theory (3rd ed.), New York: Springer Verlag, pp. section B20, ISBN 0387208607.
- Keller, Wilfrid (1995), "New Cullen Primes", Mathematics of Computation 64 (212): 1733–1741, http://www.ams.org/mcom/1995-64-212/S0025-5718-1995-1308456-3/S0025-5718-1995-1308456-3.pdf.
- Caldwell, Chris, "The Top Twenty: Woodall Primes", The Prime Pages, http://primes.utm.edu/top20/page.php?id=7, retrieved December 29, 2007.
External links
- Chris Caldwell, The Prime Glossary: Woodall number at The Prime Pages.
- Weisstein, Eric W., "Woodall number" from MathWorld.
- Steven Harvey, List of Generalized Woodall primes.
- Paul Leyland, Generalized Cullen and Woodall Numbers
|
|||||||||||||||||||||||||||||